Fungsi = Kuadrat, Rasional, Irasional

 " Fungsi = Kuadrat, Rasional, Irasional "

FUNGSI = RASIONAL 

Fungsi Rasional

Fungsi Rasional
Fungsi rasional merupakan fungsi yang mempunyai bentuk umum:

Dengan p dan d adalah polinomial dan d(x) ≠ 0. Domain dari V(x) merupakan seluruh bilangan real, kecuali pembuat nol dari d.

Adapun fungsi rasional yang paling sederhana, yakni fungsi y = 1/x dan fungsi y = 1/x².

Di mana keduanya mempunyai pembilang konstanta sertaa penyebut polinomial dengan satu suku. Dan kedua fungsi tersebut mempunyai domain semua bilangan real kecuali x ≠ 0.

Fungsi y = 1/x

Fungsi ini disebut juga sebagai fungsi kebalikan sebab setiap kita mengambil sembarang x (kecuali nol) maka akan menghasilkan kebalikannya sebagai nilai dari fungsi tersebut.

Yang artinya x yang besar akan menghasilkan nilai fungsi yang kecil, begitu juga sebaliknya. Tabel dan grafik dari fungsi tersebut bisa dilihat pada gambar di bawah ini.

Advertisement

Yang pertama, grafik tersebut lolos pada uji garis vertikal. Yang berarti setiap garis vertikal pada bidang koordinat Cartesius akan memotong grafik pada maksimal satu titik.

Sehingga, y = 1/x adalah sebuah fungsi.

Yang kedua, sebab pembagian tidak terdefinisi jadi saat pembaginya nol, maka nol tidak akan mempunyai pasangan, sehingga menghasilkan jeda pada x = 0.

Hal tersebut sesuai dengan domain dari fungsi tersebut, yakni seluruh x anggota bilangan real kecuali 0.

Yang ketiga, fungsi tersebut adalah fungsi ganjil, dengan salah satu cabangnya terletak di kuadran I.

Sementara yang lainnya berada pada kuadran III.

Kemudian yang terakhir, pada kuadran I, saat x menuju tak hingga, nilai y menuju dan mendekati nilai nol.

Secara simbolis bisa kita tuliskan sebagai x → ∞, y → 0. Secara grafis, kurva dari grafik fungsi tersebut akan mendekati sumbu-x pada saat x mendekati tak hingga.

Tak hanya itu saja, kita juga bisa mengamati bahwa pada saat x mendekati nol dari kanan maka nilai y akan mendekati bilangan real positif yang sangat besar (positif tak hingga): x → 0+, y → ∞.

Untuk catatan, tanda + atau – yang berada di atas akan mengindikasikan arah dari pendekatan. Yakni dari sisi positif (+) atau dari sisi negatif (–).

FUNGSI = KUADRAT 

Pengertian Fungsi Kuadrat

Fungsi kuadrat adalah sebuah fungsi polinom yang memiliki peubah/variabel dengan pangkat tertingginya adalah 2 (dua).

Secara umum fungsi kuadrat memiliki bentuk umum seperti berikut ini:

f(x) = ax2 + bx + c, a ≠ 0

dengan f(x) = y yang merupakan variabel terikat, x adalah variabel bebas, sedangkan a, dan b merupakan koefisien dan c adalah suatu konstanta.

Hal ini tentunya berbeda dengan yang dinamakan persamaan kuadrat, yang mana persamaan kuadrat memiliki variabel dengan pangkat tertingginya adalah dua dan berbentuk persamaan.

Bentuk umum dari persamaan kuadrat adalah sebagai berikut:

ax2 + bx + c = 0, a ≠ 0

dengan x adalah variabel bebas, a dan b adalah koefisien, serta c adalah konstanta.

Kembali ke materi fungsi kuadrat. Suatu fungsi sangat erat hubungannya dengan grafik fungsi.

Begitu pula fungsi kuadrat, yang memiliki grafik fungsinya sendiri. Grafik fungsi kuadrat berbentuk parabola yang dapat digambarkan menggunakan langkah-langkah tertentu.

Jenis-Jenis Fungsi Kuadrat

Sebelum kita membahas cara menggambar grafik fungsi kuadrat, akan kita bahas terlebih dahulu mengenai jenis-jenis lain dari fungsi kuadrat seperti di bawah ini:

1. Jika pada y = ax2 + bx + c nilai b dan c adalah 0, maka fungsi kuadrat menjadi:

y = ax2

yang membuat grafik pada fungsi ini simetris pada x = 0 dan memiliki nilai puncak di titik (0,0)

2. Jika pada y = ax2 + bx + c nilai b bernilai 0, maka fungsi kuadrat akan berbentuk:

y = ax2 + c

yang membuat grafik pada fungsi ini simetris pada x = 0 dan memiliki titik puncak di (0,c)

3. Jika titik puncak ada di titik (h,k), maka fungsi kuadrat menjadi:

y = a(x – h)2 + k

dengan hubungan a, b, dan c dengan h, k adalah sebagai berikut:

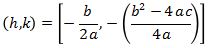
Setelah kita memahami jenis-jenis fungsi kuadrat yang lain, selanjutnya kita akan membahas cara melukis sebuah grafik fungsi kuadrat. Langkah-langkahnya sebagai berikut:

1. Menentukan sumbu simetri: x = – b/2a 
2. Menentukan titik potong kurva dengan sumbu x: misalkan y = 0, maka ax2 + bx + c = 0
3. Menentukan titik potong dengan sumbu y: misalkan x = 0, maka y = c
4. Menentukan titik puncak: 

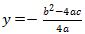
Selain itu, terdapat ciri khusus dari grafik parabola dilihat dari fungsinya. Jika a > 0 maka parabola terbuka ke atas jika sebaliknya maka parabola terbuka ke bawah.

Kemudian pada fungsi kuadrat terdapat istilah diskriminan yang memiliki bentuk:

D = b2 – 4ac

Keterangan

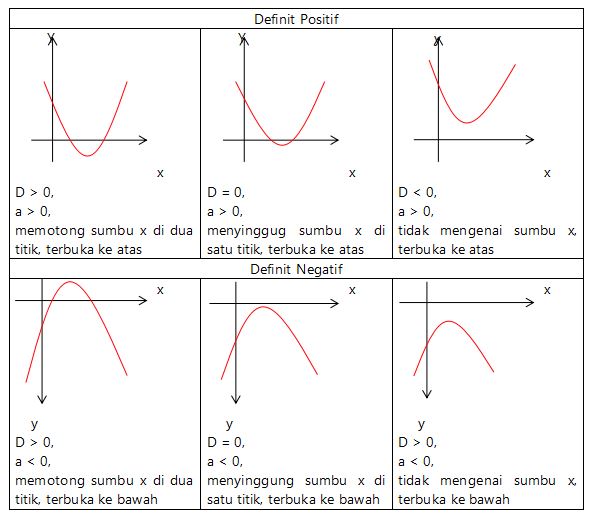
• Jika D > 0 maka fungsi kuadrat memiliki 2 akar yang berbeda dan memotong di dua titik.
• Jika D = 0 maka fungsi kuadrat memiliki 2 akar yang sama, sehingga kurva hanya akan menyinggung sumbu x di satu titik.
• Jika D < 0 maka kurva tidak menyentuh sumbu x sama sekali.

Grafik Fungsi Kuadrat

Dari ciri khusus yang dijelaskan di atas, berikut di bawah ini merupakan bentuk-bentuk grafik fungsi kuadrat secara umum beserta sedikit penjelasannya:

FUNGSI = IRASIONAL 

Fungsi irrasional adalah fungsi yang memetakan himpunan bilangan real tak negatif kepada himpunan itu sendiri. Sehingga fungsi irrasional memiliki syarat bahwa fungsi akan terdefinisi apabila nilai di dalam akar tersebut tidak negatif.

Pada fungsi tersebut terlihat bahwa fungsi tersebut irrasional yang di dalam akar memiliki bentuk pecahan biasa, sehingga dalam pecahan biasa memiliki syarat penyebut tidak boleh bernilai .

Dengan demikian, agar fungsi  terdefinisi, maka nilai  haruslah  .